The physical implementation of the Liar’s Paradox is a buzzer

by Hazard

From a delightfully weird little book, Diamond: A Paradox Logic¹:

Is the Liar true or false? Boolean logic cannot answer. What bold expedient would decide the question? What but Experiment? Let us be scientific! Is it possible to build a physical model of formal paradox using simple household items, such as (say) wires, switches, batteries and relays? Yes, you can! And indeed it’s simple! It’s easy! Just wire together a spring-loaded relay, a switch, and a battery, using this childishly simple circuit:

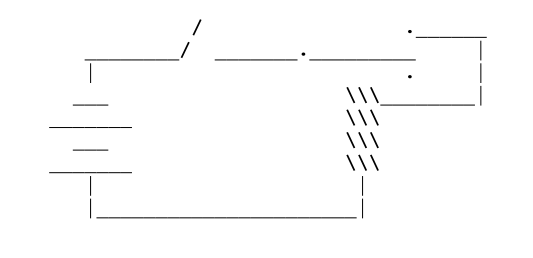
When you close the switch, the relay is caught in a dilemma; for if current flows in the circuit, then the relay shall be energized to break the circuit, and current will stop; whereas if there is no current in the circuit, then the spring-loaded circuit will re-connect, and current will flow. Therefore the relay is open if and only if it is closed. Which? To find out, close the switch. What do you see? You would see less than you’d hear; for in fact you would see a blur! The relay would oscillate. It would vibrate. It would, in fact, buzz!

“All buzzers, bells, alternators, and oscillators are based on this principle of oscillation via negative feedback. Thermostats rely on this principle; so do regulators, rectifiers, mechanical governors, and electromagnetic emitters. Electric motor/generators and heat engines are rotary variants of this process; they use cybernetic phase alternation to ensure that the crankshaft constantly tries to catch up to itself.

There’s nothing paradoxical about a buzzer circuit. Unless of course you had some notion that it was supposed to be representing things in such a way that it always ended up in some steady state. The Liar’s Paradox is a paradox because it is an intent of the representational system that is formal logic that proofs terminate. If you find that proofs in your formal system are “oscillating”, its equally logically valid to say “well I defs don’t want my proof system to do that, so time to rework the proof system” as it is to say “huh, maybe I want to think about the idea of ‘proof’ and what types of things it pertains to differently.”